数学って、本当に役に立つの?
「大人になったら数学なんて使わない」という話題は、SNSでもよく見かけます。
特に三角関数や微積分は「何の役に立つのかわからない」という声が多いものです。
実際、数学を専門に研究している人も、「これを研究して何の意味があるの」と思ってるらしいです。

画像の出典:QuizKnock 鶴崎修功が数学を研究するワケ「役に立つって思ってませんよ」
https://web.quizknock.com/tsurusaki_interview_2?page=2
(最終アクセス:2025年12月16日)
数学を勉強していても、なかなか現実世界との関連を見つけにくいところはあるかもしれません。
とはいえ、数学が実際に実生活で役に立ってる例も多くあります。
数学の本質的な力は
「わからないものを、わかっているものから導き出す」
という点にあると思っており、この力は実世界でもとても重要です。
これは机上の話ではなく、私たち製造業の現場でも、まさに“数学が役立つ例”として日々現れています。
この記事では、実際に 数学が金型設計の現場でどのように役立ったのか をご紹介します。
それを通じて、数学が役に立つ具体的なイメージをもってもらえればと思います。
数学が役立つ例 図面に載っていない寸法を導き出す
当社ではプレス加工による金属部品の成形を行っています。
そして、下記のような弓形というか弧状の金属部品をプレス加工でつくることになりました。

プレス加工をするときには、金型が必要になるので、こういう形を成形できる金型を作る必要があります。
さて、その時には金型のサイズを検討します。
部品の図面に書かれた寸法を参考にするのですが、この時の図面には下記写真のようにa、bにあたる部分の寸法しか書かれていませんでした。
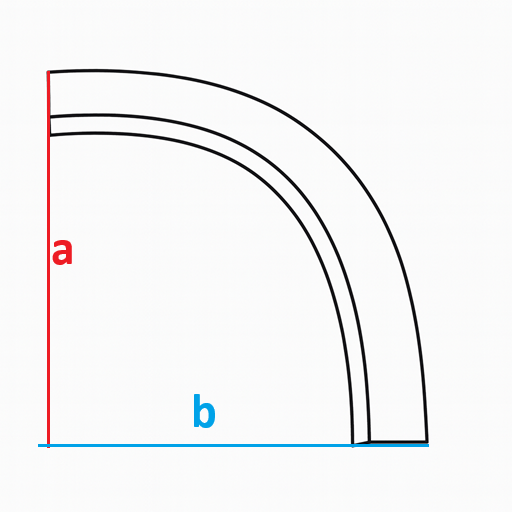
金型は、部品そのものよりも大きくないといけません。
a と b の寸法だけを基準に金型のサイズを見積もるとすると、a,b より大きめに金型をつくることになります。
すると、画像の赤枠のような範囲を金型にすることになります。
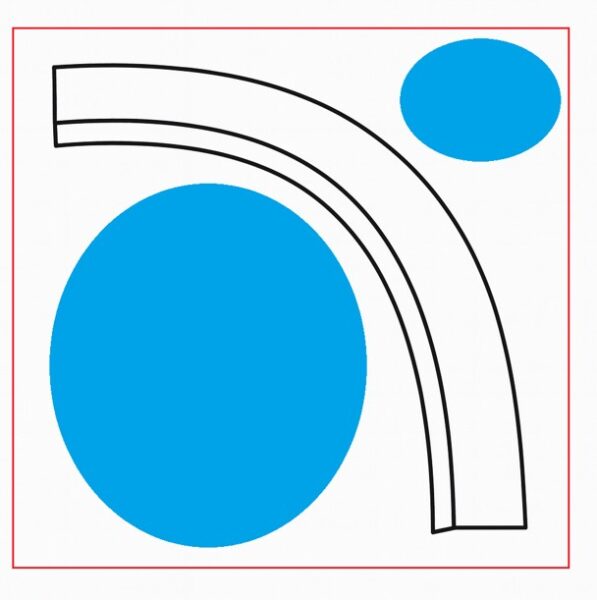
しかし、見て明らかなように無駄なスペースが多いです。
図中の青い丸で示したエリアは部品の成形に全く関与しない無駄なスペースになります。
こういう無駄なスペースが多いと、金型の材料費がムダになってしまいます。
というわけで、
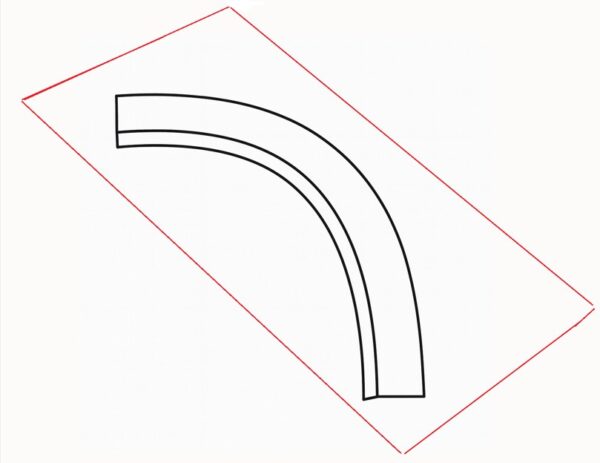
こういうイメージで金型を作るほうが、無駄がなく経済的です。
そうなると、適切なサイズの金型をつくるためには、部品の c の寸法が必要になります。
金型は部品自体より大きく作らないといけないので、cの寸法以上に幅を取る必要があるからです。
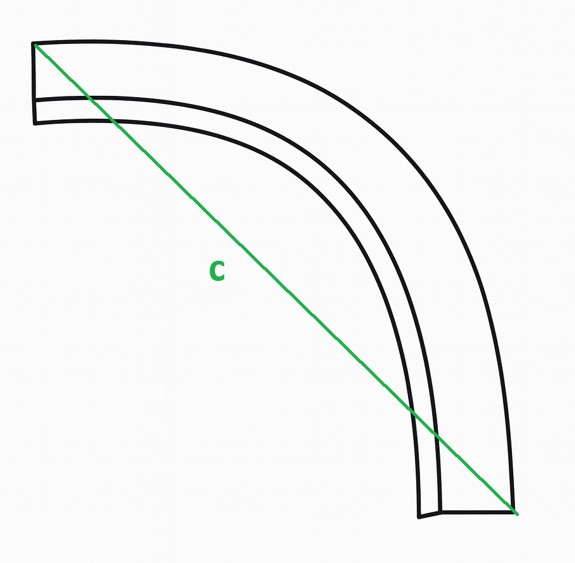
しかし、上記のように図面には a と b の寸法は書いてあるのに、金型を作るうえで必要なcの寸法はかかれていません。
そこで、このcを求めるためにどうしたらいいか?ということが問題になります。
数学(ピタゴラスの定理)が“未知を既知から導く”
さて、寸法cが図面からは直接わからない場合どうするか?ここでまさに数学が役にたちます。
よく観察すると、
a と b がちょうど直角を構成する関係 になっています。
そして、求めたい c は
a と b の端点を結んだ“斜めの直線距離”。
つまり、cはそのまま 直角三角形の斜辺 です。

ここで役に立つのが、あの「ピタゴラスの定理」
中学校で習った、あの有名な公式。
a² + b² = c²
これを使えば、
図面に書かれていない c の寸法を計算で導くことができます。
a と b は図面に載っている。
それぞれを二乗して足し、
その合計の平方根をとれば c が求まります。
たとえば、a が500mm , b が650mm なら、cはおおよそ820.061mm ぐらいと求められます。
図面には無い c を、数学を使って自力で導き出すことができました。
これでよりムダのない(つまり、費用が安い)金型が製造できるようになります。
これはまさに
「数学が役立った瞬間」
だと思っています。
数学の力は「未知を既知から導くこと」
製造業の現場では今回のように
直接は計測できない情報を、別の情報から算出する
という場面が日常的に発生します。
三角関数、微積分なども同様で、
-
測れない
-
計れない
-
直接見えない
といったものを推論するための道具です。
教科書の勉強だけでは、実生活との関連を感じられず「これが何の役に立つのだろう」と疑問に感じることも当然です。
だから、今回の事例のように、ある程度実生活と近い環境で役立つ例を示すことで、数学というものがいかに役に立ってるか実感がわいてくれればと思います。
あわせて読まれている記事:
もし、修理やメンテナンスを要する金型があるなら、すぐご相談ください。
どこよりも早い返信でお客様の時間をムダにしません。
私たちのユニークなところは、緊急時のダウンタイムを減らすための事前準備(NDAの締結など)も強く推奨していることです。
多くのお客様が私たちの考えに賛同し、「今は修理が必要な金型はないけど、とりあえずNDAだけ先に結びたい」とご連絡くださいます。
ブログ記事に関連して、「うちではこんな取り組みをしている」「この記事に関してもっと話が聞きたい」「こういう悩みがある」などの要望も沢山いただいております。
私たちKANAGATAYAはよりたくさんの情報発信をしていこうと考えてます。
より多くのニーズに応えられるようにするため、いつでもブログ記事に関する感想、意見などを受け付けております!
ご感想なども下記のお問い合わせから!

